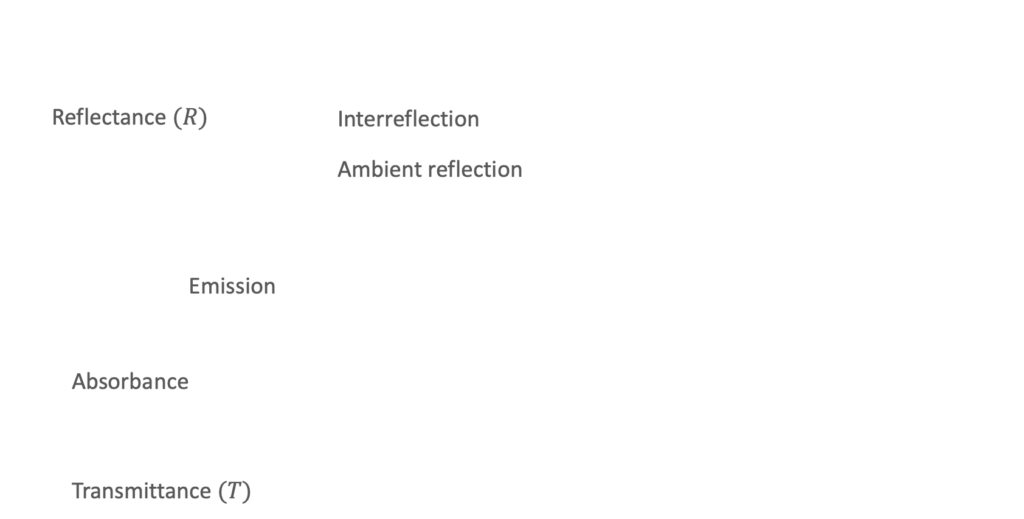
Reflection Model
Bidirectioanl Reflectance Distribution Function (BRDF)
- Lambertian Refrection Model
- Phong Refrection Model
- Blinn-Phong Reflection Model
- Cook-Torrance Refrection Model
- Oren-Nayer Reflection Model
- Torrance-Sparrow Model
- Bidirectional Texture Function (BTF)
Bidirectional Subsurface Reflectance Distribution Function (BSSRDF)
BRDF
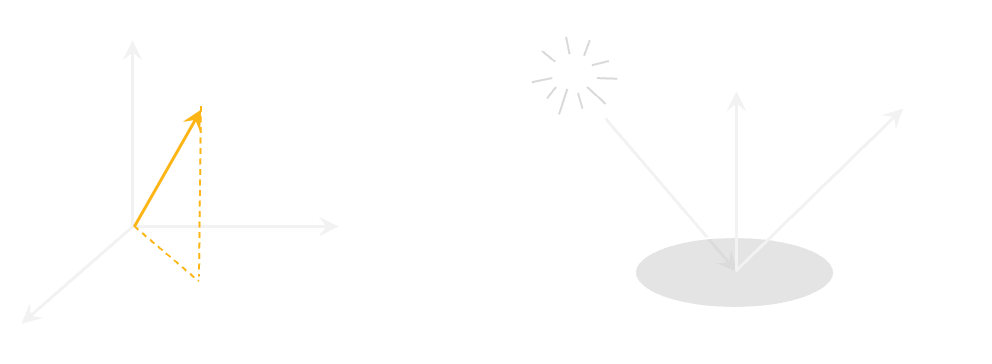
$$
f(\theta_i, \phi_i, \theta_r, \phi_r)=\frac{L(\theta_r, \phi_r)}{E(\theta_i, \phi_i)}
$$
\(f(\theta_i, \phi_i, \theta_r, \phi_r)\) is BRDF which showing reflectance from incoming direction \(\theta_i, \phi_i)\) to outgoing direction \(\theta_r, \phi_r)\).
\(L(\theta_r, \phi_r)\) is the radiance in the outgoing direction \(\theta_r, \phi_r)\).
\(E(\theta_i, \phi_i)\) is the irradiance from the incident direction \((\theta_i, \phi_i)\).
BSSRDF
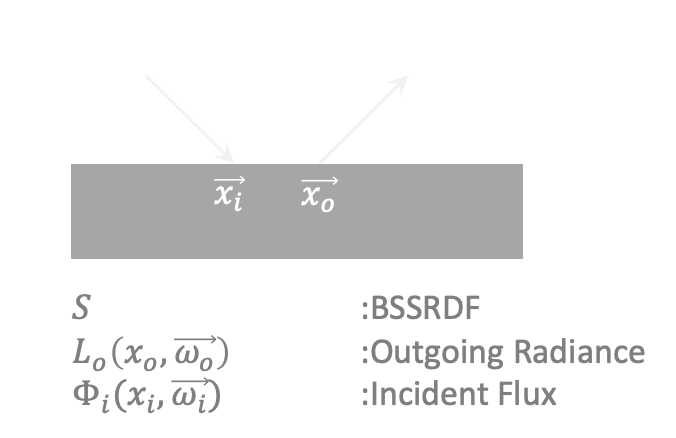
Outgoing radiance equation:
$$
dL_o (x_o , \vec{\omega_o})=S(x_i, \vec{\omega_i} ; x_o, \vec{\omega_o})d\mathbf{\Phi_i}(x_i, \vec{\omega_i})
$$
Integrating the incident radiance over incoming direction and area:
$$
dL_o (x_o , \vec{\omega_o})=
\int_{A} \int_{2\pi}
S(x_i, \vec{\omega_i} ; x_o, \vec{\omega_o})L_i(x_i, \vec{\omega_i})
\, \, d\omega_i dA(x_i)
$$
where \(A\) is the area and \(2\pi\) is the incident light flux from hemisphere.