Light Flux
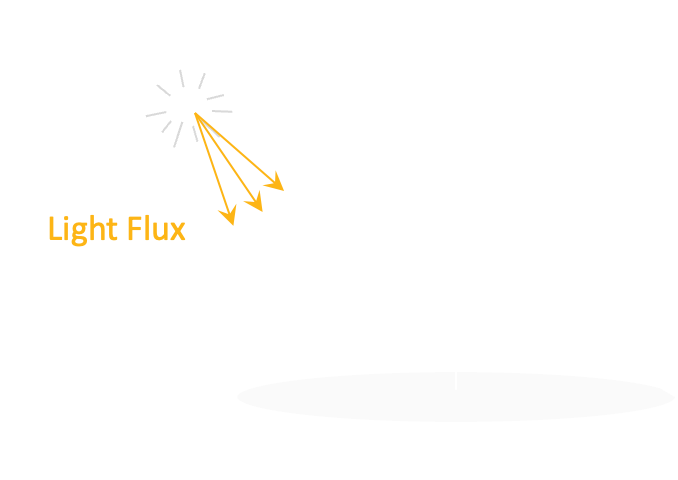
Light flux \(d\Phi\) is a power emitted within a solid angle \(d\omega\).
Unit: watts \(\mathrm{W}\)
Radient Intensity
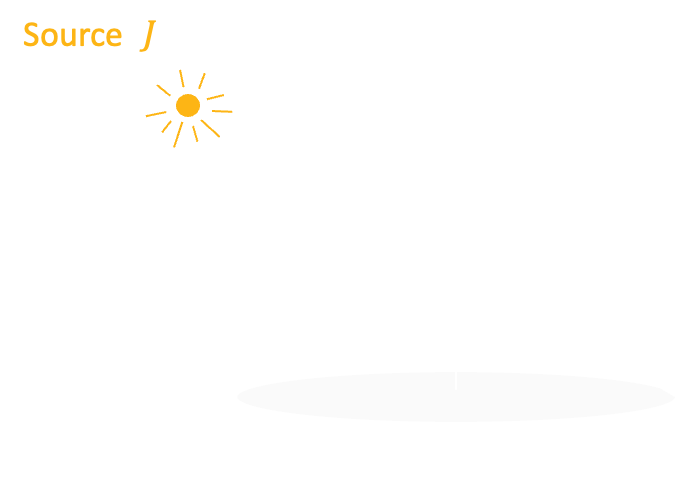
Radiant intensity \(J\) is the brightness of point light source, is the light flux emitted by the light source per unit solid angle \(d\omega\) expressed as:
$$
J=\frac {d\Phi}{d\omega}
$$
Unit: \(\mathrm{W\, sr^{-1}}\)
Surface Irradiance
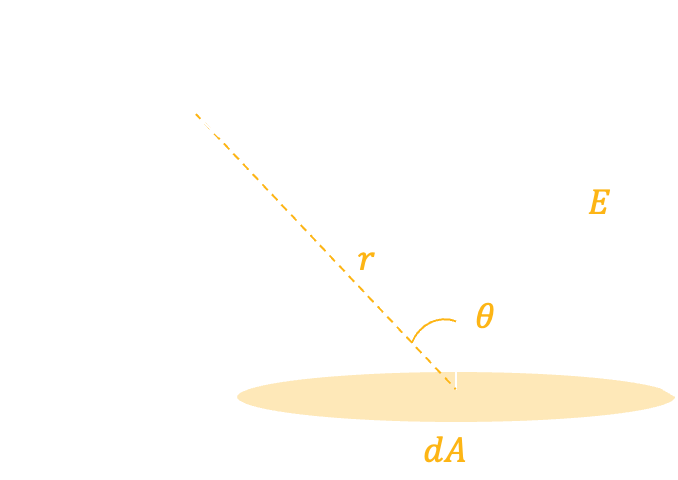
Surface irradiance \(E\) is the illumination of the surface \(dA\). Now, we have radiant intensity \(J\), and its some distance \(r\) from the surface expressed as:
$$
E=\frac{d\Phi}{dA}
$$
Unit: \(\mathrm{W\, m^{-2}}\)
This equation express that surface irradiance \(E\) is equals to the light flux \(d\Phi\) falls to the surface per unit area of the surface \(dA\).
Then we can use radiant intensity \(J\) equation:
$$
d\Phi=J\, d\omega
$$
And, solid angle \(d\omega\) express as:
$$
d\omega =\frac{dA\cos\theta}{r^2}
$$
Plug into the surface irradiance \(E\), then we get:
$$
E=\frac {J\, d\omega}{dA}=\frac {J\frac{dA\cos\theta}{r^2}}{dA}=\frac{J\, \cos\theta}{r^2}
$$
This says the strength of the illumination of the surface (surface irradiance \(E\)) is related to the radiant intensity \(J\) and one over r squared (\( \frac{1}{r^2}\)) fall-off (known as the “inverse-squared law”) times \(\cos\theta \), which is the angle of the surface normal \(\mathrm{n}\) and the light source \(J\). Therefore, when the light source is at the top of the surface (\(\mathbf{n} = \mathbf{s}, \, \mathbf{n} \cdot \mathbf{s} > 0\)), the surface irradiance becomes maximum (\(\cos \theta=1\)).
Surface Radiance
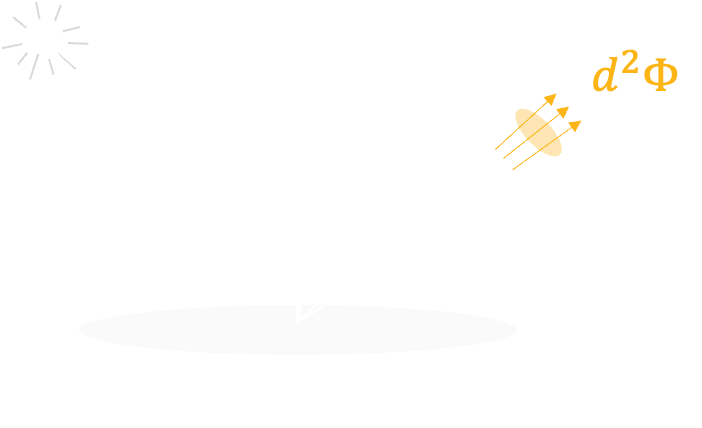
Surface radiance \(L\) is the brightness each point of the surface itself, defined as the light flux \(d\Phi\) emitted per unit foreshortened area \(dA\cos\theta _r \) per unit solid angle \(d\omega\) written as:
$$
L=\frac{d^2\Phi}{(dA\cos\theta _r)d\omega}
$$
Unit: \(\mathrm{W\, m^{-2}}\, \mathrm{sr^{-1}}\)
This is an important concept, because let consider the observed brightness of the each point acquired by the camera censor, the brightness of each point is the light flux reaching the sensor normalized by the surface area and solid angle.
[Extension] Surface Irradiance from Hemisphere
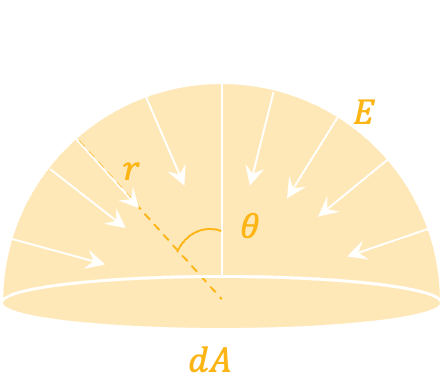
The surface irradiance at a point on the tangent place is the sum of the incident light flux from all hemisphere described as:
$$
E=\int_{\omega} L_i \, \cos\theta\, d\omega_i
$$
[Extension] Surface Irradiance with All Wavelength
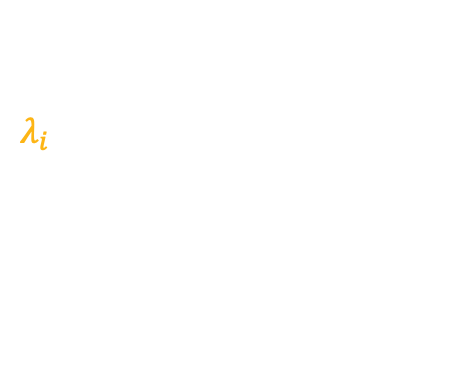
If we consider all the wavelength of light then written as:
$$
E=\int_{\lambda} \int_{\omega} L_i \, \cos\theta\, d\omega_i\, d\lambda_i
$$
Radiance Properties
Radiance \((L)\) is constant as it along ray expressed as:
$$
d \omega_1 = \frac{dA_2}{r^2}, \, d \omega_2 = \frac{dA_1}{r^2} \\
d \omega_1 dA_1=d \omega_2 dA_2 \\
L_1=L_2
$$
Relationship between Image Irradiance \((I)\) and Scene Radiance \((L)\)
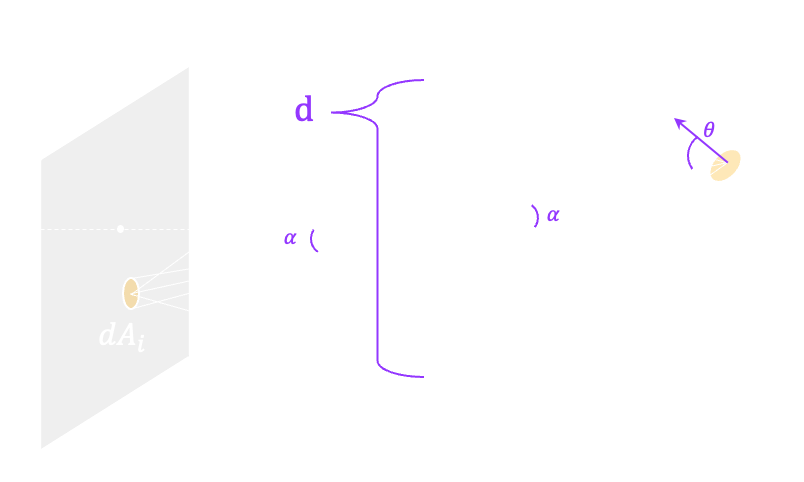
Scene radiance \((L)\) is then falls as image irradiance \((I)\).
$$
d \omega_i = d \omega_s \\
\frac{dA_i \cos\alpha}{(f/ \cos \alpha)^2}=\frac{dA_s \cos\alpha}{(z/ \cos \alpha)^2} \\
\frac{dA_s}{dA_i}=\frac{\cos \alpha}{\cos \theta}\left(\frac{z}{f} \right)^2
\tag{1} \\
$$
$$
d \omega_L=\frac{\pi \mathbf{d}}{4} \frac{\cos\alpha}{(z/ \cos \alpha)^2} \tag{2} \\
\ast dA=\frac{\pi \mathbf{d}}{4} \\
\ast r^2=(z/ \cos \alpha)^2
$$
$$
L=\frac{d^2\Phi}{dA_s \cos \theta}d\omega_L \\
I=\frac{d \phi}{dA_i} \\
L(dA_s \cos\alpha)d\omega_L=IdA_i \tag{3}
$$
$$
\boxed {I=L \frac{\pi}{4} \left(\frac{d}{f} \right)^2 \cos^4 \alpha}
$$
This equation tells you that
- Image irradiance \((I)\) is proportional to scene radiance.
- Small field of view effects of 4th power of cosine are small.